IDENTITAS TRIGONOMETRI

 IDENTITAS TRIGONOMETRI

Identitas trigonometri sebenarnya merupakan sebuah rumus yang memuat hubungan atau relasi sebuah fungsi dengan fungsi trigonometri lainnya. Lingkaran dengan pusat O (0, 0) dan jari-jari (r), sedangkan titik A (x, y) pada lingkaran dan sudut dibentuk oleh OA terhadap sumbu X. Pada berlaku r2 = x2 + y2 sehingga diperoleh perbandingan trigonometri, yaitu antara lain sebagai berikut ini :

Untuk membuktikan kebenaran dari sebuah relasi, terdapat 3 cara yang dapat kamu lakukan. Pertama adalah dengan mengubah dan menyederhanakan ruas kanan sampai ruas kanan memiliki bentuk yang sama dengan ruas kiri. Kedua, menyederhanakan ruas kiri menggunakan identitas sebelumnya sampai memiliki bentuk yang sama dengan ruas kanan. Ketiga, mengubah ruas kiri dan kanan menjadi bentuk yang sama.

MACAM – MACAM RUMUS IDENTITAS TRIGONOMETRI

Trigonometri juga memiliki beberapa macam rumus, yaitu seabagi berikut ini :

1. Rumus Jumlah Dan Selisih Dua Sudut

• Rumus Untuk Cosinus Jumlah Selisih Dua Sudut :

cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B

• Rumus Untuk Sinus Jumlah Dan Selisih Dua Sudut :

sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B

• Rumus Untuk Tangen Jumlah Dan Selisih Dua Sudut :

tan A (A + B) = tan A + tan B/1 – tan A x tan B
tan A (A – B) = tan A – tan B/1 + tan A x tan B

2. Rumus Trigonometri Untuk Sudut Rangkap

• Dengan Menggunakan Rumus sin (A + B) Untuk A = B :

sin 2A = sin (A + B)
= sin A cos A + cos A sin A
= 2 sin A cos A
Jadi, sin 2A = 2 sin A cos A

• Dengan Menggunakan Rumus cos (A + B) Untuk A = B :

cos 2A = cos (A + A)
= cos A cos A – sin A sin
= cos 2A – sin 2A ……………(1)

Atau

Cos 2A = cos 2A – sin 2A
= cos 2A – (1 – cos 2A)
= cos 2A – 1 + cos 2A
= 2 cos 2A – 1………………(2)

Atau

Cos 2A = cos 2A – sin 2A
= (1 – sin 2A) – sin 2A
= 1 – 2 sin 2A………………(3)

Dari Peramaan (1), (2), (3) diatas didapatkan rumus yaitu :

Cos 2A = cos 2A – sin 2A
= 2 cos 2A – 1
= 1 – 2 sin 2A

• Dengan Menggunakan Rumus tan (A + B) Untuk A = B :

tan 2A = tan (A + A)
              = tan A + tan A/1 tan A x tan A
              = 2 tan A/1 – tan 2A
Jadi, tan 2A = 2 tan A/1 – tan 2A

RUMUS-RUMUS YANG PERLU DIPAHAMI

• Rumus Dasar yang Merupakan Kebalikan

• Rumus Dasar yang Merupakan Hubungan Perbandingan

• Rumus Dasar yang Merupakan Turunan Dari Teori Phytagoras

CONTOH SOAL

1. Sin 75^o Cos 15^o = ….?

Jawaban:

Pada contoh soal di atas diketahui bahwa sudut A= 75^o dan sudut B= 15^o. Dengan demikian, rumusnya adalah:

Jadi, jawaban dari soal Sin 75^o Cos 15^o adalah

2. Cos 105^o Cos 15^o = ….?

Pada contoh soal di atas diketahui bahwa sudut A= 105^o dan sudut B= 15^o. Dengan demikian, rumusnya adalah:

Jadi, jawaban dari soal Cos 105^o Cos 15^o adalah

3. Tan 105^o + Tan 15^o = ….?

Jawaban:

Pada contoh soal di atas diketahui bahwa sudut A= 105^o dan sudut B= 15^o. Dengan demikian, rumusnya adalah:

Catatan:

Nilai Sin 120^o dan Cos 120^o, lihat tabel teori garis sumbu pembatas kuadran mendatar (180^o).

4. Cos 105^o + Cos 15^o = ….?

Jawaban:

Pada contoh soal di atas diketahui bahwa sudut A= 105^o dan sudut B= 15^o. Dengan demikian, rumusnya adalah:

5. Sin 105^o – Sin 15^o = ….?

Jawaban:

Pada contoh soal di atas diketahui bahwa sudut A= 105^o dan sudut B= 15^o. Dengan demikian, rumusnya adalah:

6. Perhatikan segitiga siku-siku PQR pada gambar di bawah ini!

Contoh soal trigonometri kelas 10-gambar segitiga siku-siku via Dok. Pribadi

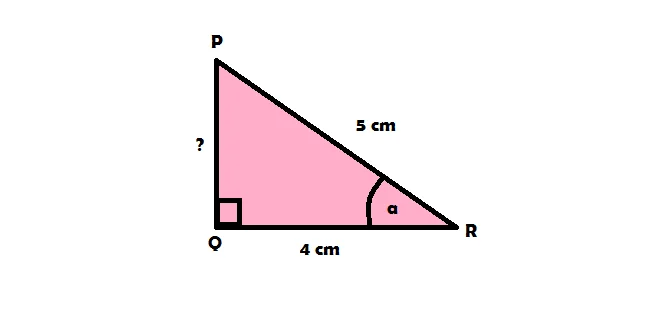
Ditanyakan:

Tentukan nilai dari sin a, tan a, cosec a, dan sec a!

Jawaban:

Sebelum menjawab pertanyaan tersebut, cari terlebih dahulu nilai dari sisi PQ. Gunakan rumus phytagoras untuk mencarinya.

Adapun rumus mencari sisi PQ pada phytagoras adalah:

Jadi, panjang sisi PQ adalah 3 cm.

*Nilai Sin a….?

*Nilai Tan a….?

*Nilai Cosec a….?

*Nilai Sec a ….?

7. Ada sebuah segitiga dengan nilai Tan A = 3/4, sedangkan A merupakan sudut lancip. Berapakah nilai dari 2Sin A + Cos A=…?

Jawaban:

Diketahui bahwa Tan A = 3/4 dengan sudut A adalah sudut lancip, maka gambarnya adalah sebagai berikut:

Gambar segitiga sku-siku via Dok. Pribadi

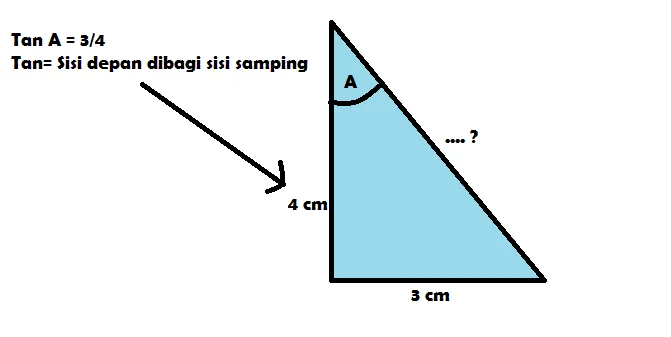
Mencari nilai dari sisi miring, gunakan rumus phytagoras yaitu sebagai berikut:

8. Jika persamaan 2 Sin² x + 3 Cos X = 0, berapakah nilai x …?

Jawaban:

Ingat, teori identitas phytagoras menyatakan bahwa: Sin²x + Cos²x = 1 sehingga Sin²x = 1 – Cos²x.

Dengan demikian, bentuknya menjadi seperti di bawah ini:

2 Sin² x + 3 Cos x = 0

2 (1- Cos² x) + 3 Cos x = 0

2 – 2 Cos² x + 3 Cos x = 0 (Kalikan dengan -1 agar persamaannya menjadi positif)

2 Cos² x – 3 Cos x – 2 = 0 (Difaktorkan)

(Cos x – 2) (2 Cos x + 1) = 0 (hasil pemfaktoran)

Maka Cos x = 2 atau Cos x = -1/2

Selanjutnya, cek manakah nilai x yang sesuai dengan syarat di atas.

9. Diketahui persamaan Sin a + Cos a = 2p, maka nilai dari 2 Sin a Cos a = …?

Jawaban:

Teori identitas phytagoras: Sin² a + Cos² a = 1

Cara perhitungannya adalah sebagai berikut:

Sin a + Cos a = 2p

(Sin a + Cos a)² = (2p)²   –> Kuadratkan kedua sisinya

Sin² a + 2 Sin a Cos a + Cos² a = 4p²

1 + 2 Sin a Cos a = 4p²

2 Sin a Cos a = 4p² – 1

Jadi, nilai dari 2 Sin a Cos a adalah 4p² – 1

Untuk menjawab soal tersebut, gunakan rumus identitas ganda di bawah ini:

Cos 2A = 1 – 2 Sin² A

Sin 2A = 2 Sin A Cos A

Dengan demikian, perbandingannya akan menjadi:

DAFTAR PUSTAKA

https://blog.elevenia.co.id/identitas-trigonometri/

https://www.dosenpendidikan.co.id/identitas-trigonometri/

https://narmadi.com/id/contoh-soal-trigonometri-kelas-10/

https://rumus.co.id/identitas-trigonometri/