LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN COSINUS
LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN COSINUS
Luas Segitiga Dengan Trigonometri
Garis AB pada segitiga ABC pada gambar di atas adalah alas segitiga. Sedangkan tinggi segitiganya adalah CD. Maka, luas segitiga ABC pada gambar dapat dihitung melalui persamaan di bawah.
Demikianlah, diperoleh persamaan yang yang dapat digunakan untuk menentukan luas segitiga sembarang dengan memanfaatkan fungsi sinus. Dengan mengikuti langkah yang sama, akan diperoleh tiga persamaan berbeda yang dapat digunakan untuk menghitung luas segitiga sembarang.
Phytagoras saat mencari tinggi segitiga

Berikutnya menentukan luas segitiga. 4 kelompok rumus berikut untuk menentukan luas suatu segitiga.

Luas segitiga dengan rumus pertama:

2. Segitiga samasisi ABC dengan panjang sisi 12 cm diperlihatkan gambar berikut!

Tentukan luas segitiga dengan menggunakan rumus nomor 3 di atas!
Pembahasan
Cari setengah dari keliling segitiga terlebih dahulu

Masuk rumus nomor tiga

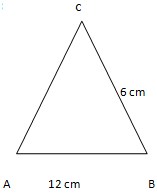
3. Segitiga sama sisi ABC dengan ukuran diperlihatkan gambar berikut!

Tentukan luas segitiga!
Pembahasan
Satu sudut diketahui beserta dua sisi pengapitnya, gunakan rumus dari kelompok 2.
4. Jajargenjang PQRS diperlihatkan pada gambar berikut!

Panjang PQ adalah 10 cm dan QR adalah 8 cm. Sudut PQR = 60°. Tentukan luas jajargenjang PQRS!
Pembahasan
Jajar genjang tersusun dari dua buah segitiga, yaitu segitiga PQR dan segitiga PSR yang luasnya sama.

Sehingga luas jajargenjang sama dengan dua kali luas salah satu segitiga.

5. Segitiga PQR diperlihatkan gambar berikut.

Jika luas segitiga PQR adalah 24 cm2 tentukan nilai sin x
Pembahasan
Dari rumus luas segitiga ditemukan nilai sin x

Aturan Sin dan Cos
Aturan sin
Aturan cos
Sehingga aturan cosinus berlaku untuk setiap segitiga ABC sebagai berikut:a2 = b2 + c2 - 2 bc cos Ab2 = c2 + a2 - 2 ac cos Bc2 = a2 + b2 - 2 ab cos C Maka di dapatkan rumus untuk menghitung besar sudutnya :
Contoh Soal
1. Diketahui segitiga ABC, dengan panjang AC = 25 cm, sudut A = 60°, dan sudut C = 75° jika sin 75° = 0,9659, tentukan panjang BC dan AB
Jawaban :

2. Pada segitiga ABC, sisi AC = 16 cm, AB = 8 √2 cm, sudut B = 45° tentukan sudut-sudut segitiga ABC yang lainnya.
Jawaban :

3. Diketahui segitiga ABC, dengan panjang BC = 4 cm, AC = 6 cm dan sudut C = 60°, tentukan panjang sisi AB
Jawaban :

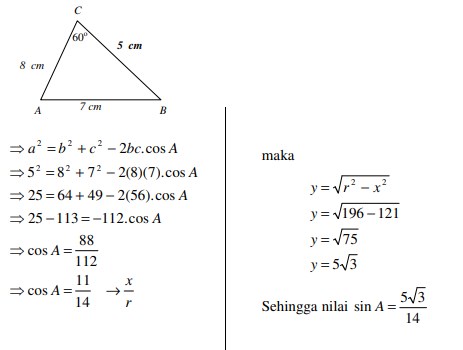
4. Diketahui segitiga ABC, dengan AB = 7 cm, AC = 8 cm, BC = 5 cm, tentukan sin A
Jawaban :
5. Tentukan luas segitiga ABC, jika diketahui AB = 15 cm, BC = 10 cm, ∠ B = 30°
Jawaban :
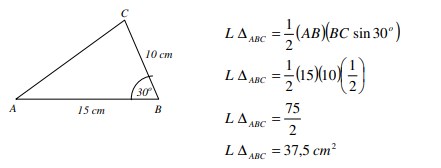




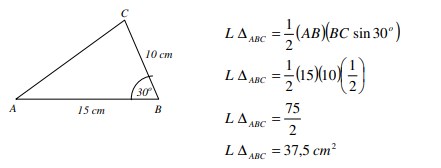
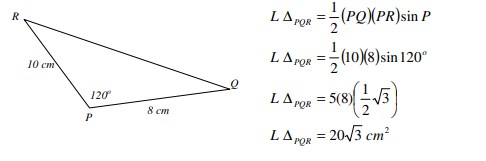
6. Tentukan luas segitiga PQR, jika diketahui ∠P = 120°, panjang PR = 10, PQ = 8 adalah. . .
Jawaban :
7. Hitunglah luas segitiga ABC, dengan panjang sisi-sisinya a = 3 m, b= 8 m, c = 9 m adalah. . .
Jawaban :

8. Luas segi 12 beraturan dengan jari-jari lingkaran luar 8 cm adalah….
A. 192 cm2
B. 172 cm2
C. 162 cm2
D. 148 cm2
E. 144 cm2
Jawaban :

9. Diketahui bahwa segitiga ABC memiliki sudut A=60 0 dan sudut B=300 dengan garis AB = 140 dan AC = 80, berapa panjang garis CB ?
Jawaban :
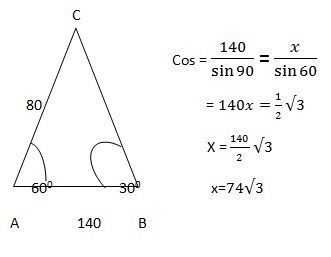
10. Dengan ketentuan Sudut CAB = 30,BCA = 90 tentukan garis AC ?
Jawaban :
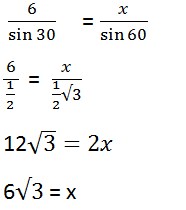



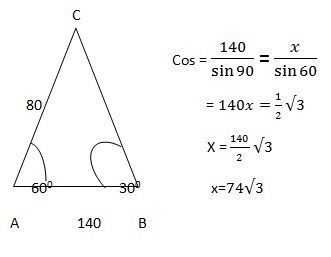

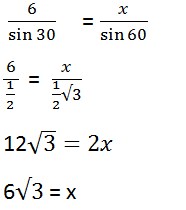
11. Diketahui segitiga PQR siku – siku di Q dengan <P = 300 dan panjang sisi PQ = 4 cm , hitunglah panjang PR ?
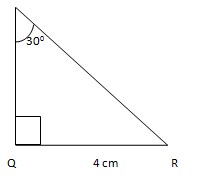
Jawaban :
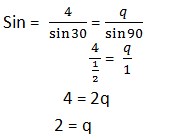
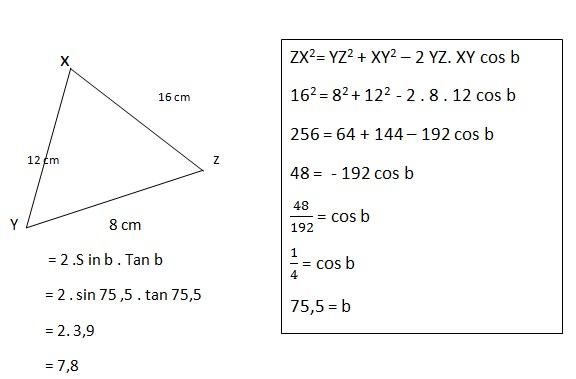
12. Sebuah segitiga XYZ dengan panjang XY = 12 , YZ = 8 , ZX= 16 . jika diketahui B merupakan sudut yang terbentuk antara sisi YX dan YZ . Maka nilai 2 Sin B. Tan B ?
Jawaban :
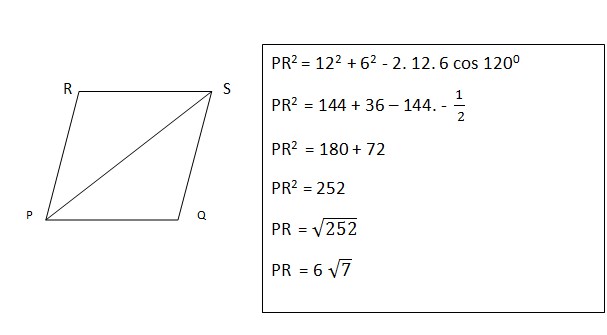
13. Sebuah jajar genjang PQRS dengan panjang QR = 12 cm dan RS = 6 cm sudut q = 1200 , maka panjang garis PR ?
Jawaban :
14. Hitunglah Panjang tali busur pada juring PKL = 1350 dengan jari – jari 10 cm ?
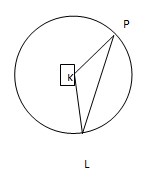
Jawaban :
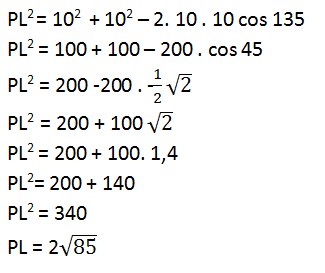
15. Berapa Luas dari segi tiga berikut ?
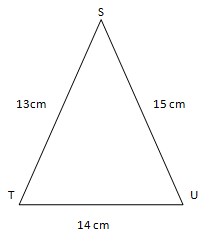
Jawaban :
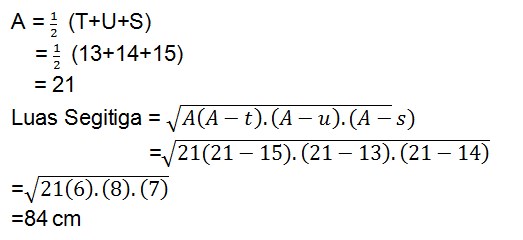

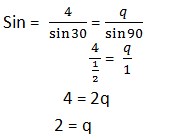



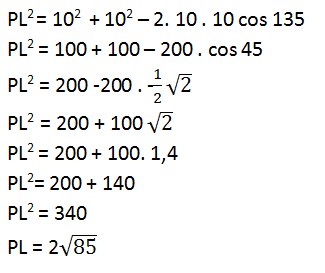

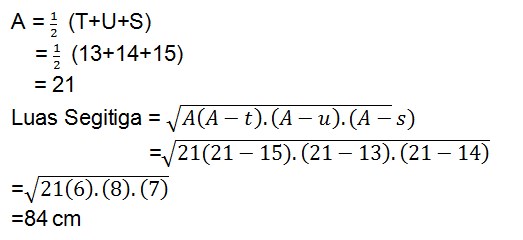
16. Tentukan perbandingan trigonometri pada segitiga berikut adalah. . .
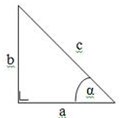
Jawaban :

17. Tentukan perbandingan trigonometri pada segitiga berikut adalah. . .
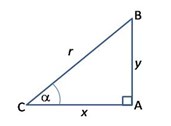
Jawaban :

18. Segitiga siku-siku berikut ini. Dengan nilai a = 4 dan c = 3 tentukan nilai sin, cos, dan tan adalah. . .
Jawaban :
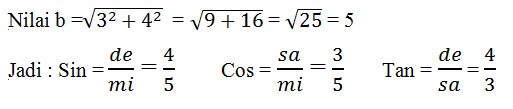
19. Diketahui sin A=0,6 dan A sudut lancip. Tentukan Cos A adalah . . .
Jawaban :
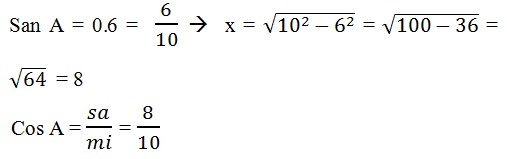
20. Diketahui sin A=0,6 dan A sudut lancip. Tentukan Tan A adalah . . .
Jawaban :
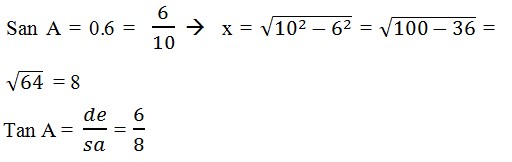




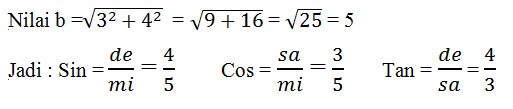
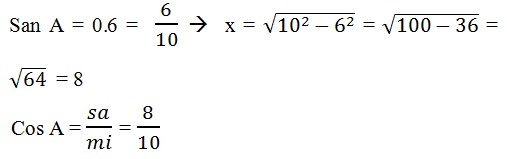
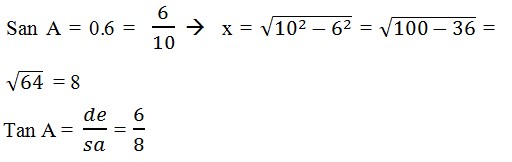












Komentar
Posting Komentar