Soal dan Pembahasan Fungsi Trigonometri
Soal dan Pembahasan Fungsi Trigonometri
Gambar di atas mempunyai persamaan ...
Jawab :
Grafik di atas adalah grafik cosinus.
Bentuk umum fungsinya adalah y = k . cos a (x ± α)
k = 3
Maka persamaan yang memenuhi grafik di atas adalah y = 3 cos x
2. perhatikan grafik berikut!
Persamaan dari grafik di atas adalah...
Jawab :
Grafik di atas adalah grafik sinus.
Bentuk umum fungsinya adalah y = k . sin a (x ± α)
k = -1
Maka persamaan yang memenuhi grafik di atas adalah y = -sin x
3. Nilai maksimum dari fungsi y = 2 sin (x + 600) + 1 adalah...
Jawab :
y = 2 sin (x + 600) + 1
y = 2 (1) + 1 = 3 (nilai maksimum)
y = 2 (-1) + 1 = -1 (nilai minimum)
4. Nilai minimum dari fungsi y = -2 cos 3/2 x adalah...
Jawab:
y = -2 cos 3/2 x
y = -2 (1) = -2 (nilai minimum)
y = -2 (-1) = 2 (nilai maksimum)
5. Nilai maksimum dari fungsi y = sin x – 1 adalah...
Jawab :
y = sin x – 1
y = 1 – 1 = 0 (nilai maksimum)
y = -1 – 1 = -2 (nilai minimum)
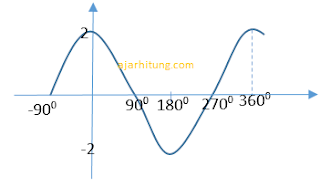
6. Perhatikan grafik berikut!
Persamaan grafik di atas adalah...
Jawab :
Grafik di atas adalah grafik cosinus.
Bentuk umum fungsinya adalah y = k . cos a (x ± α)
k = 2
Maka persamaan yang memenuhi grafik di atas adalah y = 2 cos (x + 1800)
7. Nilai minimum dari y = ½ cos x adalah...
Jawab :
y = ½ cos x
y = ½ (1) = ½ (nilai maksimum)
y = ½ (-1) = - ½ (nilai minimum)
8. Garis x = 900 dan x = 2700 pada grafik fungsi y = tan x disebut...
Jawab :
Pada grafik fungsi y = tan x saat x = 900 dan x = 2700 membentuk garis asimtot.
9. Titik koordinat dari fungsi trigonometri f(x) = sin 2x pada x = -1200 adalah...
Jawab :
f(x) = sin 2x
f(-1200) = sin 2 (-1200)
= sin -2400
= sin –(1800 + 600)
= - sin -600
= ½ √3
10. Grafik yang benar untuk f(x) = sin 2x adalah...
Jawab:
f(x) = sin 2x
f(00) = sin 2(00) = sin 00 = 0 maka titiknya (00, 0)
f(300) = sin 2(300) = sin 600 = ½ √3 maka titiknya (300, ½ √3)
f(900) = sin 2(900) = sin 1800 = 0 maka titiknya (900, 0)
Gambar yang sesuai adalah A.
11. Perhatikan gambar berikut!
Persamaan grafik fungsi di atas adalah...
a. y = 3 cos 2x
b. y = -3 cos 2x
c. y = 3 cos ½ x
d. y = -3 cos ½ x
e. y = -3 cos 2x
Jawab:
Grafik di atas adalah grafik cosinus.
Bentuk umum fungsinya adalah y = k . cos a (x ± α)
k = -3
Maka persamaan yang memenuhi grafik di atas adalah y = -2 cos 2x
12. Nilai minimum dari fungsi trigonometri f(x) =sin (2x + 300) adalah...
a. -1
b. 0
c. 1
d. 2
e. 3
Jawab:
f(x) =sin (2x + 300)
y = 1 (nilai maksimum)
y = -1 (nilai minimum)
Jawaban yang tepat A.
13. Diketahui f(x) = cos (2x - 300). Nilai yang benar untuk x = 1950 adalah...
a. 2
b. 1
c. 0
d. -1
e. -2
Jawab:
f(x) = cos (2x - 300)
f(1950) = cos (2(1950) - 300)
= cos (3900 – 300)
= cos 3600
= 1
14. Pada segitiga ABC lancip, diketahui cos A = 4/5 dan sin B = 12/13 maka sin C = ...
a. 20/65b. 36/65
c. 56/65
d. 60/65
e. 63/65
Jika cos A = 4/5, maka: sin A = 3/5 (didapat dari segitiga siku-siku berikut ini:
(ingat ya, bahwa cos itu samping/miring dan sin itu depan/miring)

Jika sin B = 12/13 maka cos B = 5/13 (didapat dari segitiga siku-siku berikut ini:

Maka, sin C = sin A . cos B + sin B . cos A
= 3/5 . 5/13 + 12/13 . 4/5
= 15/65 + 48/65
= 63/65
Jawaban: E
b. -1
c. 2 - √3
d. 1
e. 2 + √3
b. 26/63
c. 16/63
d. 6/33
e. 1/33
Sin A = 12/13, maka cos A = 5/13 (carilah dengan segitiga siku-siku seperti soal nomor 1)
Cos B = 3/5, maka sin B = 4/5 (carilah dengan segitiga siku-siku seperti soal nomor 1)

Jawaban: C
b. 1/9 √3
c. 1/2
d. – 1/3 √3
e. -√3
Perhatikan segitiga siku-siku berikut ini:

Jika cos β = -1/2 √3 maka tan β = - 1/√3 (karena di kuadran II maka nilainya negatif) jangan lupa untuk merasionalkannya:

Jawaban: D
b. 8/7
c. 7/8
d. – 8/25
e. – 8/7
Cos (A – B) = cos A . cos B + sin A . sin B
3/5 = 7/25 + sinA . sinB
Sin A . sin B = 3/5 – 7/25
Sin A . sin B = 15/25 – 7/25
Sin A . sin B = 8/25
Maka:

Jawaban: B
b. – 1/5 √5
c. 0
d. 1/5 √5
e. 3/5 √5

Misal tan x = p, maka:

(2p – 1) (p + 2) = 0
p = ½ atau p = -2 atau:
tanx = ½ atau tan x = -2
Karena ½ π < x < π atau 90 < x < 180 berada di kuadran II, ini berarti nilai tan harus negatif, maka nilai tanx yang memenuhi adalah -2.
tanx = -2, perhatikan segitiga siku-siku di bawah ini:

sehingga sinx = 2/√5 dan cosx = - 1/√5 (ingat, di kuadran II cos negatif)

Jawaban: D
b. ½
c. 1/3 √3
d. ½ √2
e. ½ √3
Perhatikan segitiga berikut:

Luas ABC = ½ . AB . AC . sin A
24 = ½ . 12 . 8 . sin A
24 = 48 sin A
Sin A = 24/48
Sin A = ½
A = 30
Maka cos A = cos 30 = ½ √3
Jawaban: E
b. 36√3 cm2
c. 144 cm2
d. 432 cm2
e. 432√3 cm2
Yuk, ingat kembali rumus luas segi-n dengan panjang jari-jari lingkaran luar r:

Maka luas segi dua belas di atas adalah:

L = 12 x ½ x 144 x sin 30
L = 12 x 72 x ½
L = 6 x 72
L = 432 cm2
Jawaban: D
b. 7 cm
c. 49 cm
d. 89 cm
e. √129 cm

= 64 + 25 – 80 . ½
= 64 + 25 – 40
= 89 – 40
= 49
a = √49
= ± 7
Jawaban: B
24. Jika
 dan q = sin x, maka p/q = ...
dan q = sin x, maka p/q = ...
b. ½ √2
c. – √2
d. √2
e. ¼ √2
Perhatikan segi-8 berikut ini:

< AOB = 360/8 = 45
<ABO = (180 – 45) : 2 = 67,5
Sudut segi-8 atau <ABC = <ABO +<OBC = 67,5 x 2 = 135
Maka nilai dari sin x + cos x = sin 135 + cos 135
= sin (180 - 45) + (-cos (180 - 45)
= sin 45 + (-cos 45)
= ½ √2 - ½ √2
= 0
Jawaban: A
b. –r
c. 0
d. R
e. 2r
sin (Q + P) = r
sinQ . cosP + sinP. cosQ = r
1.cos P + 0 = r (ingat ya, diketahui Q = siku-siku)
Cos P = r ... (i)
Sin R = sin (180 – (Q + P)
= sin (Q + P)
= r
Maka, cos P – sin R = r – r = 0
Jawaban: C
b. – ½ √3 dan 2/3 √3
c. ½ √3 dan – 2/3 √3
d. – 1/3√2 dan – 2/3√3
e. 1/3√2 dan 2/3 √3

Misalkan sin x = A, maka:

(2A – 1) (3A + 1) = 0
A = ½ atau A = - 1/3
Maka, sin x = ½ , maka cos x = 1/2 √3
Sin x = - 1/3, maka cos x = 2/3√2
Jawaban: A
b. 1/3 √3
c. ½ √3
d. 2√3
e. √3
Perhatikan segitiga berikut:


= 9 + 16 – 12
= 13
BC = √13
Maka, kita cari nilai cos B:

Aplikasikan pada segitiga siku-siku:

tan <ABC = 2√3/1 = 2√3
Jawaban: D
b. 1/3 √6 p
c. ½ √6 p
d. 2/3√6 p
e. √6 p
Perhatikan segitiga berikut:

Segitiga ACT siku-siku di T, maka kita dapat mencari panjang sisi CT dengan rumus phytagoras:

Maka, panjang BC :

Jawaban: E

Bila digambarkan, maka soal diatas menjadi:

<ABC = 30 + 90 = 120
Kita cari panjang AC:

= 900 + 3600 + 1800
= 6300
AC = √6300
= 30√7
Jawaban: B

Perhatikan segitiga berikut:


Karena <CDB + <ADB = 180 maka:
cos <CDB = - cos <ADB

Jawaban: B
33. Jika π/2 < α < π dan tan α = p, maka
 = ...
= ...
Karena π/2 < α < π maka ada di kuadran II
tan α = p, maka perhatikan segitiga di bawah ini:

jadi, tan α = -p (karena berada di kuadran II)

maka:

Jawaban: B
b. – ½
c. 0
d. ½
e. 1
Sin (y + x) = sin y . cos x + cosy . sin x
sin y . cos x = sin y . cos x + cosy . sin x
cosy . sin x = sin y . cos x - sin y . cos x
cosy . sin x = 0
Jawaban: C
b. ½ √3
c. 1/3 √3
d. – ½ √3
e. -√3
 = ...
= ...
Pembahasan:
Diingat lagi ya identitas trigonometri yang ini:

Jawaban: A
37. Jika α dan β sudut lancip, tan α = ¾ dan tan β = 1 maka nilai 5(cos (α + β) + cos (α - β) adalah ...
b. 2√2
c. 3√2
d. 5
e. 4√2
tan α = ¾, maka sin α = 3/5 dan cos α = 4/5 (gunakan segitiga siku-siku)
tan β = 1, maka sin β = ½ √2 dan cos β = ½ √2 (gunakan segitiga siku-siku)
cos (α + β) = cos α.cos β – sin α.sin β
= 4/5. ½ √2 – 3/5. ½ √2
= 4/10√2 – 3/10√2
= 1/10√2
= √2/10
cos (α - β) = cos α.cos β + sin α.sin β
= 4/5. ½ √2 + 3/5. ½ √2
= 4/10√2 + 3/10√2
= (7√2)/10
Sehingga nilai dari 5(cos (α + β) + cos (α - β) = 5 .( √2/10 + (7√2)/10 ) = 5((8√2)/10) = (40√2)/10 = 4√2
Jawaban: E














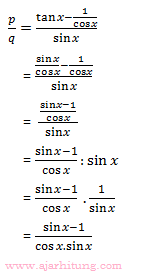












Komentar
Posting Komentar